Matrix Power Calculator

Matrix Power Calculator

(Supports Negative Powers & Exact Arithmetic)

This calculator computes the integer power of a square matrix Aⁿ using exact rational arithmetic (no floating-point errors).

It supports both positive and negative integer powers, ensuring mathematically correct results even for inverses

How it Works

• For n ≥ 0, it multiplies the matrix by itself n times using fast exponentiation by squaring (O(log n)).
• For n < 0, it first computes the exact matrix inverse via Gauss–Jordan elimination over rational numbers, then raises that inverse to ∣n∣.
• All operations are integer-safe, ensuring no precision loss.

Formula

For a square matrix A and an integer n:

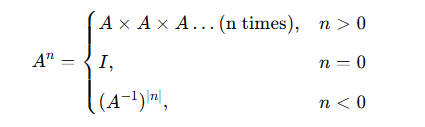
where

• A^-1 = the inverse of matrix A
• I = the identity matrix (1’s on the diagonal, 0’s elsewhere)

This means:

• Positive powers repeat multiplication.
• Zero power always gives the identity matrix.
• Negative powers first find the inverse, then apply the positive power to it.