Linear Independance Calculator
Linear Independence Calculator – Formula and Process
The Linear Independence Calculator determines whether a given set of vectors are linearly independent or dependent.
Formula
Vectors 𝑣1,𝑣2,…,𝑣𝑛 are said to be linearly independent if:
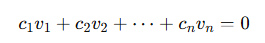
has only the trivial solution:
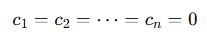
Process
-
Form a Matrix
Place the given vectors as columns in a matrix 𝐴=[𝑣1 𝑣2 … 𝑣𝑛].
-
Row Reduction (RREF)
Apply Gaussian elimination to convert 𝐴 into its Reduced Row Echelon Form (RREF).
- Each pivot (leading 1) represents a linearly independent column.
- Zero rows indicate dependent relationships.
-
Rank Test
- If the rank of 𝐴 equals the number of vectors, the vectors are independent.
- If the rank is less than the number of vectors, they are dependent.
-
Determinant Method (for square matrices only)
- If det(𝐴)≠0 → Independent
- If det(A)=0 → Dependent